Segmentation : Overview of the state of the art

1 Comment

 

Segmentation is a widespread analysis, bringing particular advantages to companies. It can be used in very different fields and sectors of activity such as health, industry, human sciences. Or in the top management too, marketing or finance departments for instance. In this article, we will focus on a generic methodology that adapts to the diversity of use cases. The first part will be devoted to the description of the process and the second to its implementation.

 

Example: American cities segmentation by socio-economic criteria click Here (generated by d3.js)

Segmentation is, by definition, the grouping and characterization of observations in homogeneous sets commonly called “clusters”. However, research and papers on the subject show that segmentation remains a difficult task, especially because of its arbitrary nature. There is a very wide range of algorithms for separating and grouping observations (unsupervised learning), and the choice of one over another is not necessarily obvious. It is also the  case of the choice of the variables to be selected, why a variable represents and / or is relevant to meet the need of the analysis? These legitimate questions do not prevent the production of quality segmentation. It is nevertheless necessary to be aware of these many biases in order to exclude any missleading interpretation or analysis.

As part of a first approach, we will be inspired by the methodology proposed by the book :  « Statistique exploratoire multidimensionnelle »  (Dunod, Paris, 1995 ISBN 2100028863).

It is carried out in several stages:

  • Dimension reduction

Dimension reduction is the analysis of compressing the information of large dataset into a small number of dimensions. There are different reduction methods, each of which has advantages and disadvantages. Principal Component Analysis (PCA) is the method used here. This algorithm uses the correlation paradigm to reduce a dataset. The advantage of using correlation is that the interpretation of the results is easier and more convenient. Although this method is rather basic, it is particularly recommended and effective for visualizing multidimensional data, while having a quantifiable and controlled loss of information.

  • Unsupervised classification

Unsupervised algorithms can be based on different metrics: entropy, distance, density. The goal is nevertheless the same:

Separate observations into homogeneous sets

The Hierarchical agglomerative clustering (HAC) used here consists firstly of assigning a class by observations and then of grouping the classes progressively according to the criterion of dissimilarity chosen. It is applied directly to the PCA coordinates generated previously.

the number of clusters

Determining the optimal number of clusters in a dataset is a fundamental problem for clustering. There is no theory definitively and absolutely solving this problem, there is always a certain degree of subjectivity. Indeed, the evaluation of the similarities varies with more or less intensity according to the method used. Nevertheless, some of these methods are now consensually accepted and commonly used.

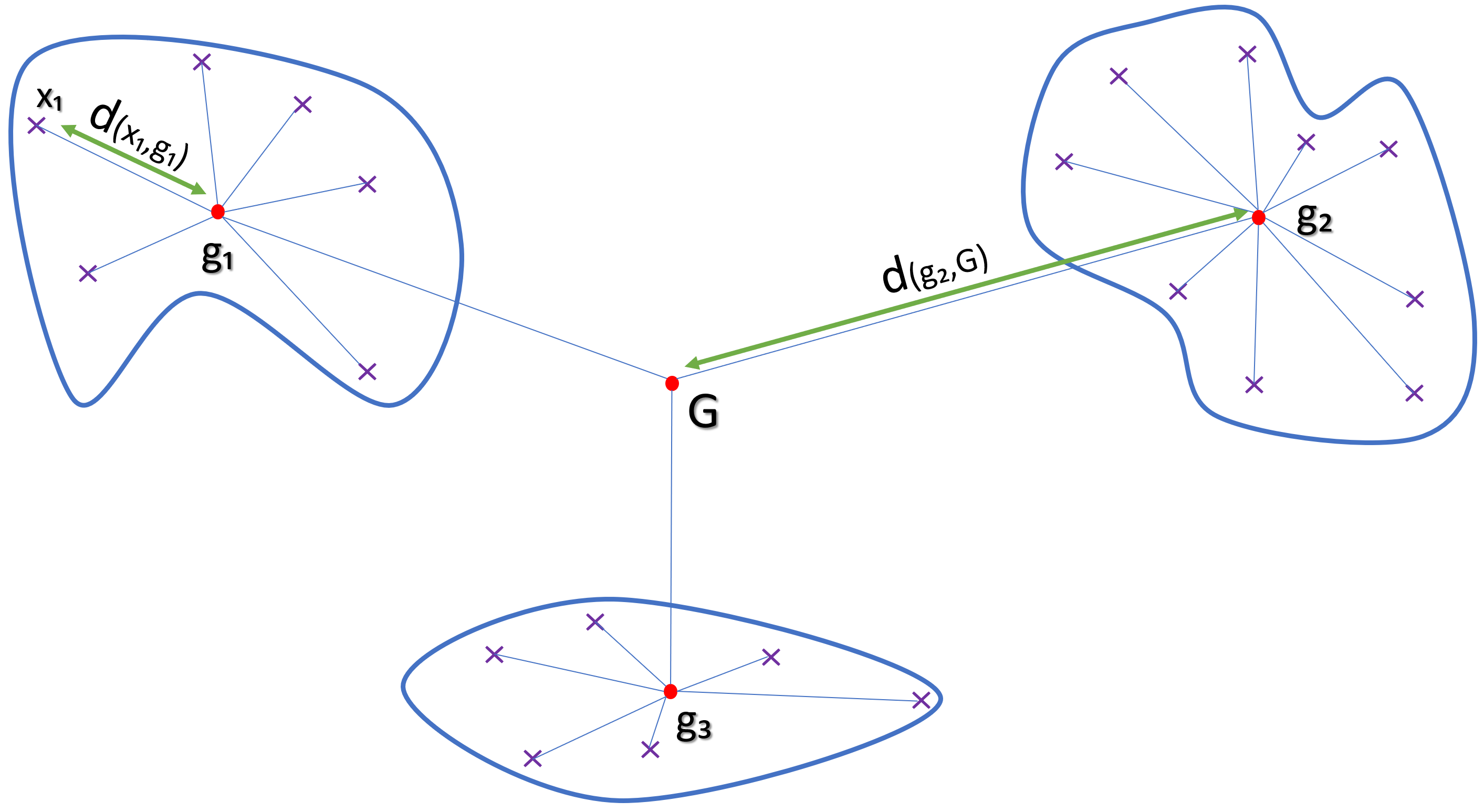
Elbow Method is probably the most used method for the simplicity of its implementation. The essence of the technique is to evaluate Within the cluster Sum of squares “wss” for each cluster with a value “k” of the number of clusters, different  each time {2, 3, 4, etc. …}.
 

Representation of inertia inter & intra cluster

Formula 

WWS : Within cluster Sum of Squares
SSB : Sum of Squares Between cluster
d(xi,gi) : Euclidian distance between  dots xi and centroid gi

The goal is to minimize inter-cluster inertia (wws), or maximize inter-cluster inertia (ssb) because the total inertia of the point cloud is the sum: Total inertia = wws + ssb

Benefits of applying unsupervised classification to PCA results.
it may seem rather surprising at first to apply the classification method to the PCA results and not to the raw data itself. However,This type of procedure has both a practical interest and a theoretical interest.
The combination procedures provide an unavailable visualization in the opposite case. We can thus have an idea of the relative positions of the observations and classes with respect to each other but also of their dispersion and their silhouette.
Another advantage is the ability to select a limited number of dimensions generated by the PCA. This is to take into account only the dimensions that have a high variance ratio explained and to leave the residual dimensions, thus avoiding potential undesirable random fluctuations. By focusing on the most relevant information, we are improving the quality of the partitions.
From a theoretical point of view, the stability of the results remains guaranteed by the fact that the sum of the eigenvalues (total inertia of the selected dimensions) of the PCA is equal to the sum of the level indices of the a Hierarchical agglomerative clustering (HAC) (Ward’s method).
This sequence also attenuates a phenomenon that takes place in large dimensions: the curse of dimensionality. The concept is developed by Richard Bellman in the 1960s, whose idea is to say to a number of equal observations, the more we add dimensions, the more we exponentially generate the void in the multidimensional space. The manipulation of large-scale data  makes the concept of distance (in the Euclidean meaning of the term) progressively meaningless. Therefore, any distance-based clustering technique can lead to suboptimal results.

 

  • Characterization of clusters
This step is often neglected, the characterization of clusters represents, in many cases, the added value of the process.
The grouping phase makes it possible to group the homogeneous observations with each other, but does not indicate in what way these sets are similar or stand out.
Again, there are several ways to compare groups with each other. The statistical tests used are often average comparison tests based on variable distribution assumptions (Student, Normal …). Others use density or more sophisticated calculations.

 

Implementation

 

To illustrate this mechanism, we will focus on segmenting certain large American cities on several criteria: social, economic, demographic etc … in order to characterize the notion of “wellness” in these cities.
 The previously described procedure has been coded in R and in JavaScript “D3.js” for a better visualization. The dataset and the code are availaible Here

 
First step:
 
Loading libraries and data sets.

library(FactoMineR)
library(factoextra)
library(ggplot2)
library(ggrepel)
library(DT)
library(jsonlite)

df=read.csv("wellness.csv", sep=";",dec=",",
row.names = 1, header= TRUE,
check.names=FALSE)

 
Second step:
 
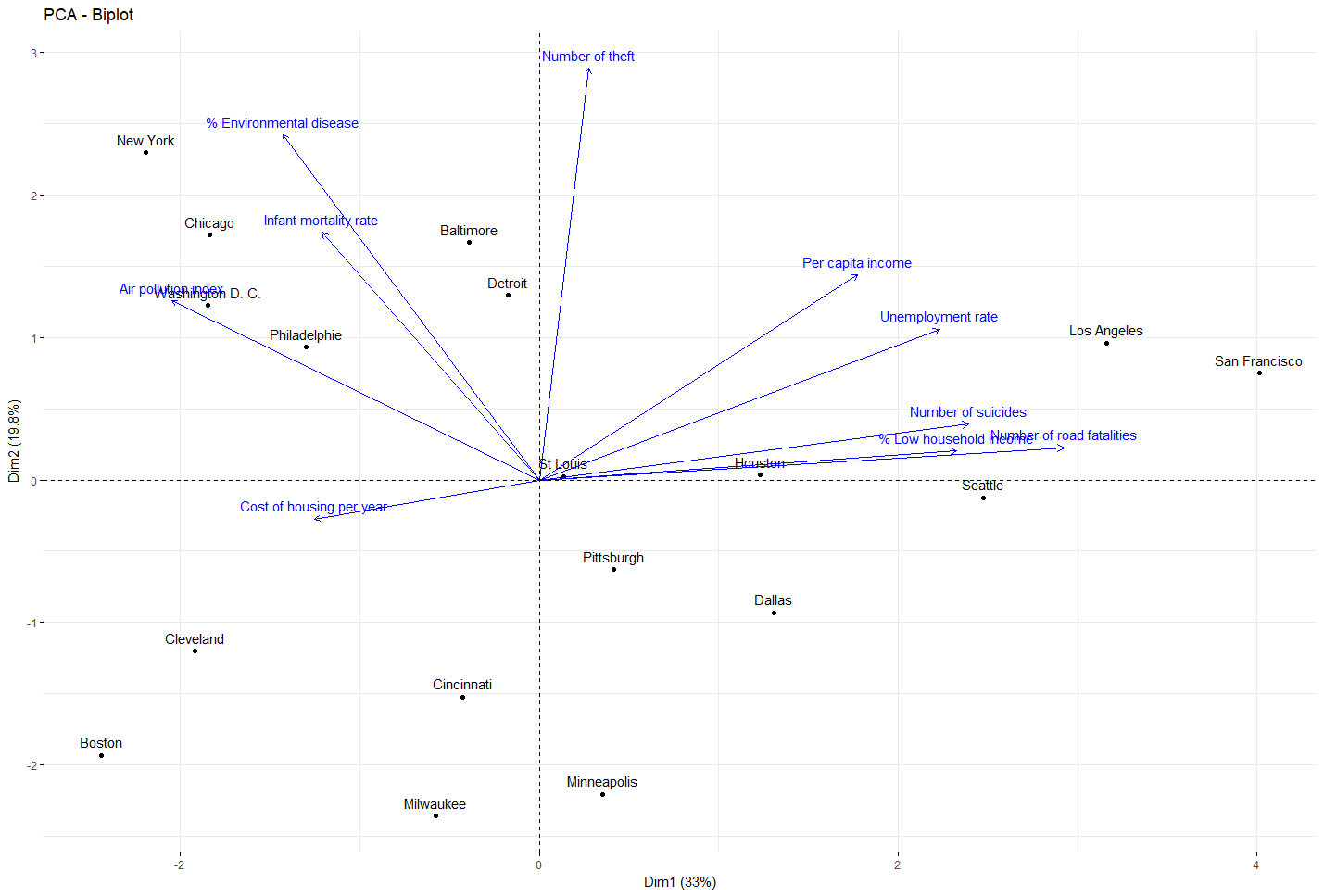
Dimension reduction through PCA and intermediate result visualization.

res_acp = PCA(df, scale.unit=TRUE, ncp=ncol(df), graph=F)
df_acp=as.data.frame(res_acp$ind$coord)
fviz_pca(res_acp, col.var ="blue")



Show  Results 




 


Clic  Here to know how to interpret the result.




 

Third step:

 

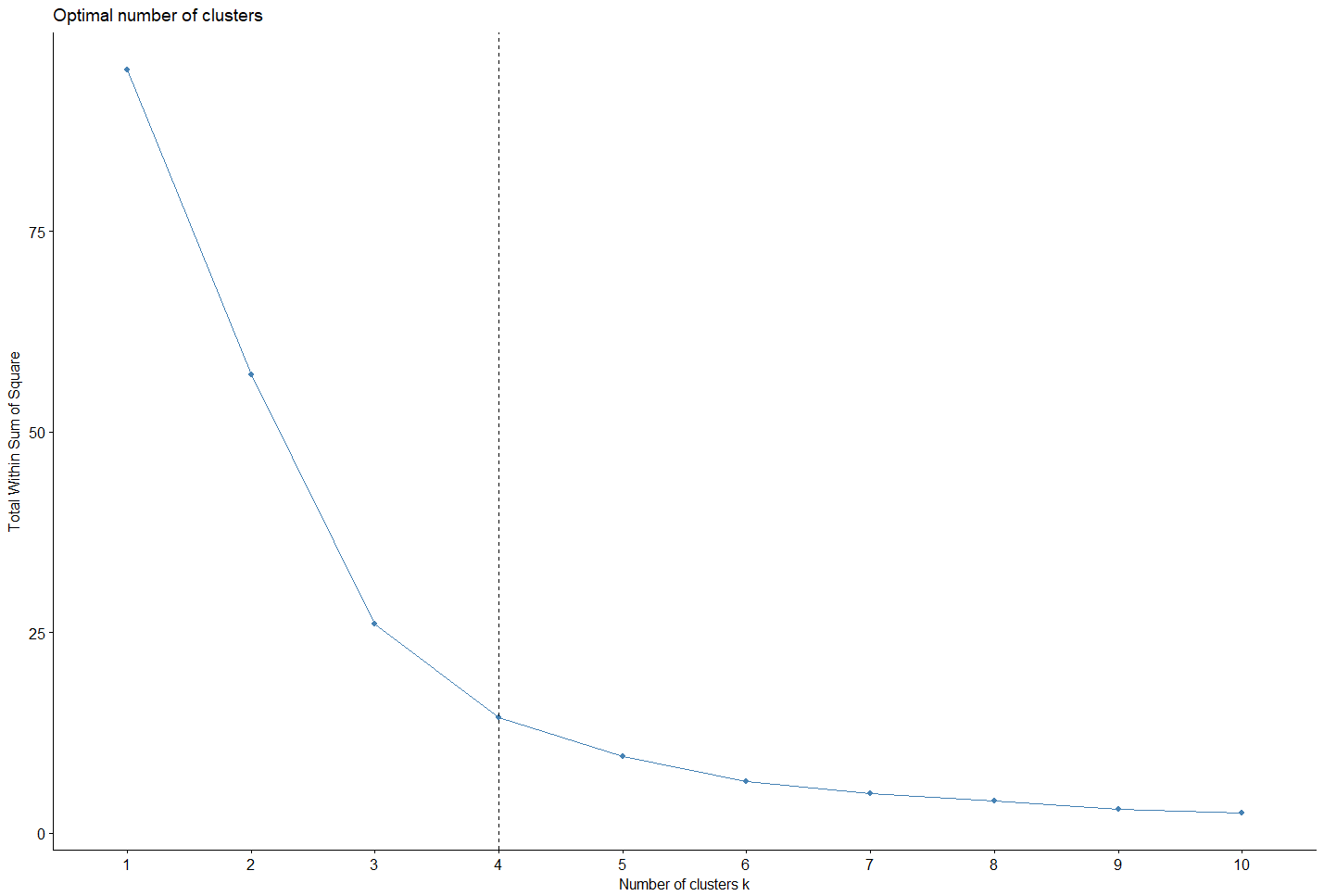
Clusterization using the HAC algorithm: The cluterization is done on the data projected through the PCA result, where the optimal number of cluster is calculated.


 
alpha= 0.20
opt_calc=fviz_nbclust(df_acp[,c(1,4)], hcut, method = "wss")

for ( i in 1:10){
   
  if(opt_calc$data$y[i+1]/opt_calc$data$y[1]<alpha){
    nb_optimal=i+1
    break
  }
}

fviz_nbclust(df_acp[,c(1,4)], hcut, method = "wss")+geom_vline(xintercept = nb_optimal, linetype = 2)
cluster=cutree(CAH, nb_optimal)
cluster=as.data.frame(cluster)
df_cluster=cbind(df_acp,cluster)


Show Results 






 

Fourth step:

 

Cluster’s characterization by z-test (normal distribution assumption)


z.test = function(k, g){
  
  n.k = length(k)
  n.g = length(g)
  Sk=((n.g-n.k)*var(g))/((n.g-1)*n.k)
  zeta = (mean(k) - mean(g)) / sqrt(Sk)
  
  return(zeta)
}

threshold=0.975
threshold.val=qnorm(threshold)

cluster_info <- data.frame(matrix(nrow=ncol(df)))
temp=data.frame()
df_c=cbind(df,cluster) 



for ( j in 1:nrow(unique(cluster))){ 
  cat("\n","cluster ", j, "\n", "\n", "\n" )
  for (i in 1:ncol(df)) {
    statistic=z.test(subset(df_c[,i], cluster==j),df_c[,i]) 
    
    temp=rbind(temp,statistic) 
    
    if (statistic >=threshold.val || statistic <= -threshold.val) {
      
      cat(colnames(df)[i],":",statistic[1],"\n")
      
    } 
    
  }
  colnames(temp)=paste("cluster",toString(j[1]) , sep=" ")  
  cluster_info=cbind(cluster_info,temp)
  temp=data.frame()
  
}



Show Result


cluster 1 
 
 
% Environmental disease : 2.971881 
Infant mortality rate : 2.332093 
Air pollution index : 1.992268 
Number of theft : 2.574825

cluster 2 
 
 
Per capita income : 2.288678 
Unemployment rate : 3.111431 
Infant mortality rate : -2.092907 
Number of suicides : 2.704074 
Number of road fatalities : 2.496167

cluster 3 
 
 
% Low household income : -2.045789 
Cost of housing per year : 2.021008 
% Environmental disease : -1.979993 
Number of theft : -2.022158

cluster 4 
 
 
% Low household income : 2.336857 
Cost of housing per year : -2.544205





 

Last step:

 

Json generation for visualization using D3.j


path_json="viz/outfile.json"
 
if (file.exists(path_json)) file.remove(path_json)

cat("{",'"features":',"[",file=path_json,append=TRUE)
for(i in 1:ncol(cluster_info)){
  
  cat('{\n"cluster":','"',i,'",','\n','"vars"',": [",'\n',file=path_json,append=TRUE)
  cluster_info=cluster_info[order(cluster_info[,i],decreasing = TRUE), , drop = FALSE]
  for(z in 1:nrow(cluster_info)){
    
    
    if(abs(cluster_info[z,i])>=threshold.val){
      cat('{','\n','"label" :','"',rownames(cluster_info)[z],'",','\n','"value":',round(cluster_info[z,i],digit=2),'\n }',file=path_json,append=TRUE)
      if(max(which(abs(cluster_info[,i])>=threshold.val))!=z) { cat(",",file=path_json,append=TRUE) }
      cat('\n',file=path_json,append=TRUE)
    }
  }
  
  cat("] \n } ",file=path_json,append=TRUE)
  if(ncol(cluster_info)!=i) { cat(",",file=path_json,append=TRUE) }
  cat("\n"  ,file=path_json,append=TRUE)
}
cat("],",'"observations": [',file=path_json,append=TRUE)
res1=df_cluster[, c(1,2,length(df_cluster))]
res1=cbind(ENTRY=rownames(df_cluster),df_cluster[, c(1,2,length(df_cluster))])
colnames(res1) <- c("name","Dim_1","Dim_2","cluster")
row.names(res1)<- NULL
x <- toJSON(unname(split(res1, 1:nrow(res1))))
x=gsub("[[]", "", x)
x=gsub("[]]", "", x)
cat(x,file=path_json,append=TRUE)
cat("\n ] \n }",file=path_json,append=TRUE)




 


Non-linear approach





 


Whether for PCA or HAC, compression or separation of data is always done in the same way: linearly. There is another category of algorithm that can compress the information of a dataset with a different approach.




One of the most famous, the T-SNE, proposed by Geoffrey Hinton and Laurens van der Maaten, uses metrics derived from information theory, using a probabilistic view of the distances between observations. It is now widely used and can be beneficial for distinguishing local patterns that can be hidden by specific characteristics of density and dispersions of a dataset.




Because of its non-linear approach, the algorithm does not maintain distances or density, but the proximity between observations is maintained.




Essentially developed for large datasets, it is nevertheless greedy in computing time and has a key parameter: the perplexity that needs to be properly calibrated.




The T-sne is a non-deterministic algorithm by repeating it several times, it is possible to have differences on the global silhouette as well as on the relative positions of the clusters. But , observations assigned to a cluster will not radically change.






To illustrate the difference in results of the PCA and T-SNE methods. We are going to press a dataset representing the behavior of the customers in a supermarket.


Code R comparing the results of the tnse with the pca


data=read.csv2("customers-data.csv",row.names = 1,header = TRUE)
data=data[,1:8]

res.pca = PCA(data, scale.unit=TRUE, ncp=ncol(df), graph=F)
res.tsne=tsne(scale(data),k = 2,max_iter = 500,epoch = 100,perplexity = 60)

km.tsne=kmeans(res.tsne,3)

par(mfrow=c(1,2))
plot(res.tsne,col=km.tsne$cluster,main="tsne")
plot(res.pca$ind$coord[,1:2],main="pca")



Running this code shows us how according the reduction method used the results vary. This allows in this case to detect indiscernible sets otherwise.


 


Differences of results between tsne and pca




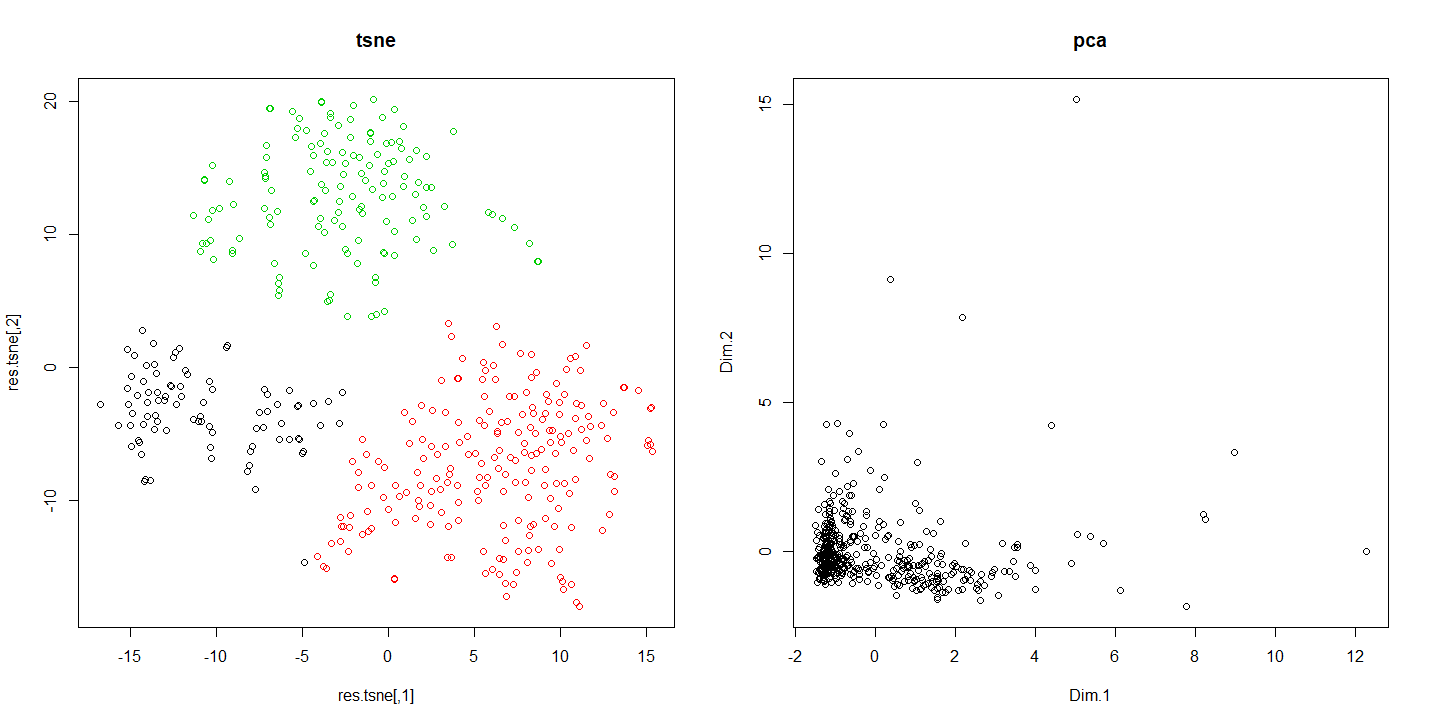
Conclusion 


The approach presented here shows a method that can be applied in many circumstances. It can be adjusted according to the characteristics of the dataset and presents the interest to be easy to intepret thanks to a set of indicators.On the other hand, this does not save us from particular vigilance, given the pitfalls that we can be confronted with in this type of exercise.


References


[1] BellmanReferences, Richard. Dynamic programming. Courier Corporation, 2013.


[2] Benzécri, Jean-Paul. L’analyse des données. Vol. 2. Paris: Dunod, 1973.


[3] Maaten, Laurens van der, and Geoffrey Hinton. “Visualizing data using t-SNE.” Journal of machine learning research 9.Nov (2008): 2579-2605.


 

	
	

		
				
	

		
One Comment

		
	
    
		
  1. 
	
    
		
    
						Julie		
    
		
     
			
					
    
		
    
			
    Very clear, even though it took me a while to understand.
    
I was lucky to have stumbled upon this post
    

    I work for a major insurance company in US. Customer profiling is very important for us and your approach is fully adaptable to our challenges.
    

    bravo! 🙂
    
Thank you very much
    
		
    
		
    
					
    
			
	
    	

    2. 	



	

		
Leave a Reply